Heap

Heap adalah sebuah objek array yang divisualisasikan sebagai complete binary tree. Bentuk Heap adalah complete Binary Tree yang mengartikan bahwa semua level diisi kecuali level terakhir.

Jenis Heap :

1. Min Heap
Setiap elemen memiliki nilai yang lebih kecil daripada node childnya. Angka terbesar dalam min heap terdapat pada salah satu node leaf (Node di level terakhir).
2. Max Heap
Kebalikan dari min Heap, setiap elemen memiliki nilai yang lebih besar daripada node childnya. Angka terkecil dalam min heap terdapat pada salah satu node leaf (Node di level terakhir).
3. Min Max Heap 
Gabungan dari min dan max heap dimana masing" level akan berganti ganti antara min heap dan maxheap.

Operasi dalam heap (Min dan Max Heap)

INSERT
untuk menambahkan suatu elemen, kita dapat melakukan operasi up-heap(heapify-up) untuk mengembalikan sifat heap dengan syarat:

1. Tambahkan elemen pada level bawah heap.
2. Bandingkan elemen yg baru ditambahkan dengan parentnya, jika mereka berada di urutan yang benar, berhenti.
3. Jika tidak, swap elemen dengan parent dan kembali ke langkah sebelumnya.

Contoh insert pada maxheap :

Menambahkan angka 15 pada (X).

Dikarenakan angka 15 lebih besar dibandingkan parentnya (8) maka tuker angka 15 dengan 8
Menukar 15 dan 8

Disini angka 15 masi melanggar syarat karena lebih besar daripada parentnya maka, tukar angka 15 dengan 11


Menukar angka 15 dengan 11

Jadilah max-heap yang benar.

REMOVE

untuk operasi remove dapat digunakan cara down-heap (heapify-down).
dengan cara mengganti root heap dengan elemen terakhir pada level terakhir. Kemudian cek apakah heapnya sesuai dengan tidak dengan syarat min atau max heap. Jika tidak sesuai, swap dengan salah satu childerennya. (Jika dalam min heap, swap dengann children yg lebih kecil, dan pada maxheap, sebaliknya swap dengan children yg lebih besar). Terus lakukan sampai sesuai dengan syarat

Contoh Remove 4 pada max heap

Valid Tree

Kemudian tree di remove sehingga angka 11 dikeluarkan
Menghapus root kemudian menukar dengan node paling akhir yaitu 4
Angka 4 sudah melanggar syarat dikarenakan lebih kecil dari child, sehingga tukar dengan child yang lebih besar (angka 8)

Jadilah Heap yang sudah lengkap dan sesuai dengan syarat.

Insert (Min-Max Heap)

Jika suatu terjadi penambahan data (insert) maka proses yang dilakukan akan dipengaruhi oleh level data tersebut.
Ketika data baru berada di level min, maka bandingkan dengan parentnya. Jika parent memiliki nilai yang lebih kecil,  dan upheapmax dari parentnya. Jika tidak, upheapmin dari posisi new node. Uphead pada minmax heap tidak membandingkan dengan parent, tetapi grandparent (parent dari parent)

Contoh penerapan jika insert pada level max
Angka 1 dimasukan, sehingga 1 merupakan new Node. Angka 1 berada pada level max, maka jika 1<10 swap.
Angka 1 dan 10 di swap.
Kemudian dari posisi 1 di upheapmin, karena 1<2 maka 1 dan 2 di swap.
Min max heap telah terpenuhi


Contoh penerapan pada level min


Angka 85 baru dimasukkan, dan angka 85 berada level min, sehingga bandingkan dengan parentnya (80). dan 85 > 80 mala swap. Kemudian 85 di upheapmax, tetapi karena 85<90, maka 85 tetap diposisinya.
Jadilah Min-max heap yang sesuai dengan syarat.



Remove(Min-maxHeap)
Remove pada min max heap ada 2 jenis yaitu remove min dan remove max. Jika min, maka root langsung dihapus, jika delete max, maka angka max dari children root akan dihapus. Jika pada delete min dimulai dari level 1, delete max dimulai dari level 2 dan dicari nilai yang paling besar untuk di remove.

Contoh dari remove min-maxheap, delete min


Angka 1 di remove, tukar dengan 80.
Angka 80 dibandingkan dengan grand childnya, yaitu 4,8,3,2. Dikarenakan angka 2 merupakan angka paling kecil. maka swap.
Kemudian cek angka 80 dengan childnya. karena 10 merupakan yang terkecil, maka swap.

 Jadilah minmax heap yang sesuai dengan syarat.

Tries

Tries adalah struktur data yang meiliki bentuk seperti pohon, biasanya menyimpan data berupa string. Tries diambil dari Retrieval, karena Tries dapat menemukan sebuah kata tunggal dengan menggunakan huruf awal. 

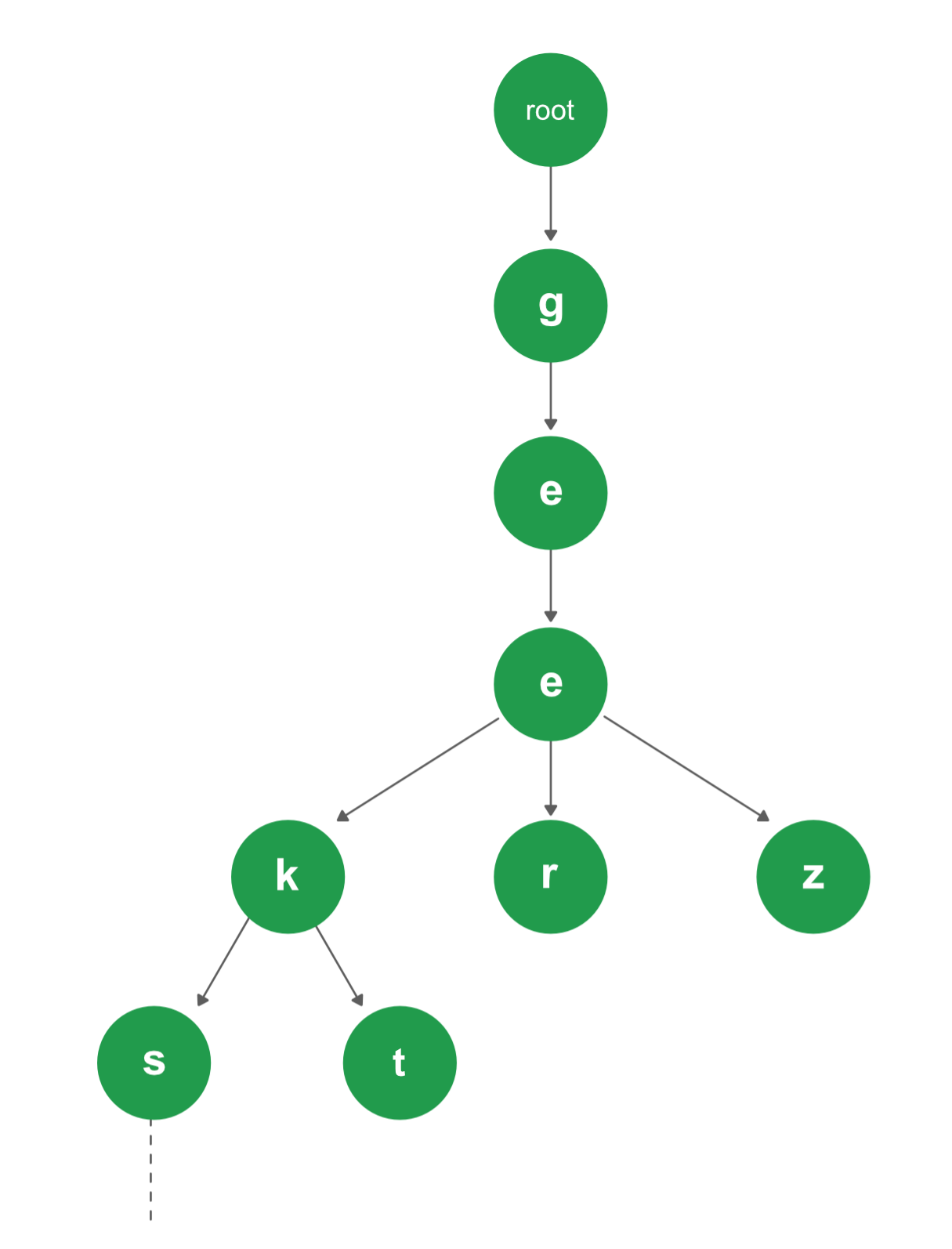
Demikian penjelasan mengenai Heap dan Tries . Terima kasi ^ ^

AVL TREE

AVL Tree adalah Binary Search Tree yang memiliki perbedaan level maksimal 1 antara subtree kiri dan subtree kanan. AVL Tree digunakan untuk menyeimbangkan BST, dengan AVL Tree waktu pencarian dan bentuk tree dipersingkat dan disederhanakan.

Berikut merupakan contoh dari AVL Tree



Angka 0 menandakan tidak memiliki perbedaan level antara subtree kiri dan subtree kanan
Angka 1 menandakan memiliki perbedaan 1 level yaitu berada pada subtree kanan (subtree kiri < subtree kanan)
Angka -1 menandakan memiliki perbedaan 1 level yaitu berada pada subtree kiri(subtree kanan < subtree kiri)

Penambahan node pada AVL tree (Insert)

Untuk menjaga BST tetap seimbang, setiap dilakukan penyisipan node, dilakukan pemeriksaan node baru. Jika tidak seimbang, maka akan dilakukan proses penyeimbangan yaitu Single Rotation dan Double Rotation.

Single Rotation

Single Rotation dilakukan bila kondisi AVL Tree waktu akan ditambahkan, searah left-left / right-right



Double Rotation

Double Rotation dilakukan bila kondisi AVL Tree berlawan arah, left-right atau right-left.

Rotasi pertama
Rotasi kedua




Penambahan node pada AVL tree (Delete)

Tidak hanya dapat melakukan insert, tetapi ada operasi lainnya bernama delete, proses delete ini dilakukan sama seperti BST yaitu node yang dihapus digantikan oleh node terbesar pada subtree kiri atau yang terkecil pada subtree kanan. Setelah dilakukan penghapusan, dicek kembali apakah tree sudah seimbang atau belum, jika tidak seimbang, maka akan dilakukan proses penyeimbangan dengan menggunakan single rotation atau double rotation.

Delete node 60

Pada node 55 tidak seimbang maka akan dilakukan single rotation

Pada node 50, tree menjadi tidak seimbang, maka dilakukan double rotation

Hasil akhir setelah dilakukan double rotation



Demikian penjelasan saya mengenai AVL Tree.